Печник (Москва)
На основании уравнений можно вывести общее уравнение для часто встречающихся на практике случаев передачи тепла от среды, находящейся с одной стороны данного тела, к среде, расположенной по другую его сторону; такая передача тепла происходит например при охлаждении помещений через наружные стены, окна, полы и потолки, так как в этом случае воздух в помещениях передает часть своей теплоты наружному воздуху через вышеуказанные ограждения помещений; тот же случай встречается при передаче тепла воздуху помещений от продуктов горения, циркулирующих по дымооборотам печей, при чем теплота передается через стенки дымооборотов.
Для вывода соответствующих уравнений, дающих зависимость между количеством передаваемой теплоты и температурой одной и другой среды, рассмотрим сначала тот случай, когда температура одной и другой среды остается постоянной на всем протяжении поверхности, передающей теплоту, взяв при этом общий случай стены, состоящей из нескольких слоев а1, а2, а3 (черт. 29) с воздушным прослойком между ними b, причем примем следующие обозначения:
Т и t-температуры среды с левой и правой стороны стены, при чем Т >t:
t1, t2, t3, t4 и t5 - температуры поверхностей соответствующих слоев;
е1, е2, е6-толщина слоев;
y1, y2 и y3 коэффициент теплопроводности этих слоев;
Q1 - коэффициент поглощения теплоты от левой среды к стене;
Q2-коэффициент потери тепла стеною к правой среде;
W- постоянное количество тепла, передающееся от одной среды к другой в 1 час через 1 кв. метр поверхности стены при установившейся передаче тепла.
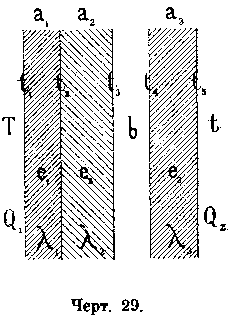
В этом случае теплота будет передаваться от левой среды к поверхности первого слоя, затем от этого последнего к следующему слою и т. д. и, наконец, от последнего слоя к правой среде, при чем будет иметь место совокупность всех рассмотренных выше явлений поглощения,теплопроводности и потери теплоты.
Количество теплоты, передающееся от левой среды к поверхности первого слоя, соответственно уравнению , будет:
W=Q1 (T-t1)
это же количество тепла передается, вследствие теплопроводности, через первый слой ко второму и через второй слой к прослойку воздуха, почему, на основании уравнения будем иметь:
W=(y1(t1-t2)) /e1
W=(y2(t1-t2)) /e2
Далее, прослоек воздуха нельзя рассматривать как слой, аналогичный предыдущим, так как воздух в прослойке не находится в покое, вследствие неодинаковой температуры его в разных частях прослойка: у поверхности второго слоя стены воздух прослойка приобретает теплоту, нагреваясь до температуры этой поверхности t3, у поверхности же третьего слоя отдает эту теплоту, охлаждаясь до температуры t4, при чем происходит падение более холодного воздуха у второй поверхности и поднятие более нагретого у первой. При этом передача теплоты воздухом в прослойке будет происходить вследствие соприкасания движущегося воздуха к поверхностям слоев и вследствие лучеиспускания, теплопроводность же воздуха не будет оказывать влияния на эту передачу. Обозначая количество тепла, передающееся соприкасанием, через n1 и принимая среднюю температуру воздуха в прослойке равною (t3+t4)/2, получим:
n1=1(t3-(t3+t4)/2))=1/2(t3-t4)
что же касается до передачи тепла через лучеиспускание, то, вследствие почти полной теплопрозрачности воздуха, вся лучистая теплота передается непосредственно от поверхности второго слоя к поверхности третьего; обозначая ее через n2, получим:
n2=s(t3-t4)
следовательно, полное количество тепла, передающееся через прослоек, будет:
W=n1+n2=(1/2+s)(t3-t4)
Для третьего слоя стены передача тепла, вследствие теплопроводности, будет:
W=(y3(t4-t5))/e3
и, наконец, передача тепла от поверхности третьего слоя к среде, находящейся по правую его сторону, будет:
W=Q2(t5-t)
Во все эти равенства входят неизвестные нам температуры поверхностей слоев; для исключения их определим из указанных равенств разности температур, при чем получим:
T-t1=W/Q
t1-t2=We1/y2 ;
t 2-е3=We2/y2 ;
t3-t4=W/(1/2+s)
t4-t5=We3/y3
t5-t=W/Q2
складывая между собой первые и вторые части , получим:
T-t=W(1/Q1+e1/y1+e2/y2+1/1/2+s+e3/y3+1/Q2)
откуда:
W=T-t/(1/Q1+e1/y1+e2/y2+1/1/2+s+e3/y3+1/Q2)
Обозначая предстоящее Т - t через К, будем иметь:
W= K(T-t)
где K=1/(1/Q1+e1/y1+e2/y2+1/1/2+s+1/Q2)
1) 1/Q- выражающих зависимость потери или поглощения тепла наружными поверхностями;
2) e/y- дающих зависимость от теплопроводности и толщины слоев и
3) 1/(1/2+s), дающего зависимость от воздушного прослойка и входящего в знаменатель столько раз, сколько прослойков имеется в данной стене.
Это указание дает возможность составлять выражение для всеобщего коэффициента передачи тепла, не прибегая в каждом отдельном случае к подробным исследованиям.
В заключение следует заметить, что если всю поверхность стены обозначим через F, то количество тепла W0, передающееся через всю поверхность, будет:
W0 = FK.(Т - t)
Раcсмотрим некоторые частные случаи определения всеобщего коэффициента.
1) Кирпичная не оштукатуренная наружная стена толщиною е == 0,64 м.
Для наружного воздуха для более неблагоприятного случая 1 = 6 для внутреннего
I1 = 5; далее по таблицам 3 и 4 будем иметь: y= 0,69, s = 3,6; наконец, соответственно
сказанному при толщине стены в 0,64 м. - разность температур между поверхностью стены и воздухом может быть принята равною 4°.
Тогда по ур.
Q1= 5 + 3,6 + (0,0075 X 5 + 0,0056 X 3,6) 4 = 8,84 Q2 = 6 + 3,6 + (0,0075 X 6 + 0,0056 X 3,6) 4 = 9,86
И, наконец, по ур.
K =1/(1/8,84+0,64/0,69+1/9,86)=0,9
2) Кирпичная наружная стена, снаружи не оштукатуренная, внутри - штукатурка и обои; толщина стены ег = 0,51 м., толщина штукатурки е2 = 0,01 м.г толщина обоев е3 = = 0,0001 м.
Согласно предыдущему примеру 1 = 6, I1 = 5; по таблице 3 и 4:
для кирпича и штукатурки S = 3,6, Y = 0,69,
обои (бумага) S= 3,8 Y = 0,034; далее при толщине стены в 0,51 метра разность температур между поверхностью стены воздухом может быть принята равною 5°.
Тогда будем иметь:
Q1 = 5 + 3,8 + (0,0075 X 5 + 0,0056 X 3,8) 5 = 9,1
Q2= 6 + 3,6 + (0,0075 X 6 + 0,0056 X 3,6) Х 5 = 9,93
K=1/(1/1/9+0,0001/0,034+(0,51+0,01)/0,69+1/9,93)=1,04
3) Окно из двух рам, с воздушным прослойком между ними, при толщине стекол 0,002 м.
Для наружного воздуха 1=6, для комнатного 1 = 5, для воздуха между рамами 1 = 4; коэффициент лучеиспускания для стекла S = 2,91, коэффициент тедлопроводности y = 0,8.
Тогда имеем:
Q1 = 5 + 2,91 + (0,0075 X 5 + 0,0056 X 2,91) X 10= 8,45 Q2 = 6 + 2,91 + (0,0075 X 6 + 0,0056 X 2,91) X 10 = 9,52
Наконец, получим:
K=1/(1/8,45+0,002/0,8+1/(4/2+2,91)+0,002/0,8+1/9,52)=2,2
Если принять, что воздух в прослойке совершенно неподвижен и расстояние между рамами = 0,18 м., то при теплопроводности воздуха, равной 0,04, получим
K=1/(1/8,45+0,002/0,8+0,18/0,04+0,002/0,8+1/9,52=0,21
В действительности, как это было уже указано, воздух в прослойке находится в постоянном движении, почему результат первого расчета следует признать более правильным.
Значение коэффициентов передачи тепла К для разного рода поверхностей, ограждающих помещения, дано в таблице, таблица эта служит преимущественно для расчета потерь тепла помещениями вследствие охлаждения через наружные ограждающие их поверхности.
Определение потерь тепла помещениями делается с целью выяснения количеств тепла, которые должны быть добавляемые в помещения для поддержания в них постоянной температуры, но при этом необходимо принимать во внимание, что помещения, расположенные на юг, получают добавочную теплоту от солнечных лучей, расположенные же на север такой добавочной теплоты не получают; в равной мере на потерю тепла помещениями оказывает влияние и направление господствующих ветров; в виду этого к потерям тепла помещениями, определенным на основании таблицы добавляются еще запасы в нижеследующем размере:
для помещений, расположенных на север, северо-восток, северо-запад и восток 15%для помещений, расположенных на запад, юго-запад и юго-восток 10%
для помещений, подверженных господствующем ветру 10%
для угловых помещений добавляется, кроме выше указанных запасов еще 5%
Пример. Определить потери тепла помещениями А и В, показанными на черт. 30 и находящимися в верхнем этаже; высота помещений 4 метра, толщина наружных стен 2,5 кирпича, потолок устроен на деревянных балках; температура воздуха в помещениях должна быть Т = 18° С., температура наружного воздуха t = -200 С., температура на чердаке t1 = -100 С помещение в расположен на север.
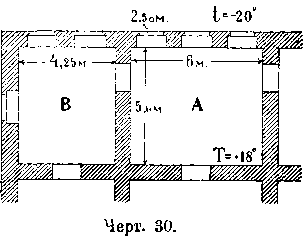
Охлаждающимися поверхностями в помещении А будут: три окна поверхностью F1=3x2,5=7.5 кв. метр., наружная стена площадьюF2=6X4-7,5=16.5 кв. метров и потолок площадью F3=6X5,6=33.6 кв. метр.; значение коэффициентов К по таблице будет: для окон K1=2,2 ед. т., для стен К2 = 0,8 ед. т. и для потолка К3 = 0,49 ед. тепла. Следовательно все охлаждение помещения будет:
W=(F1K1+F2K2)(T-t)+F3K3(T-t1)=7,5 X 2,2+16,5 X 0,85) X[18 -(-20)] X 0,49 X [18-(-10)]=1620 ед. т.,
а с добавлением 15% на страны света 1620+243=1863 ед. т.,
Определенная таким же образом потеря тепла помещением В (угловым) будет W1=1922 ед ., с добавлением 15% на страны света 1922+273 = 2195, а с добавлением 5% на угловое помещение 2195+110 = 2305 ед. т.
Формула справедлива для передачи тепла через стену при условии, что температура одной и другой среды постоянна на всем протяжении поверхности стены; однако, если эта температура и не постоянна,но изменяется на протяжении всей поверхности стены незначительно, то и в этом случае можно, без большой погрешности, пользоваться формулою , приняв температуру среды равною средней арифметической температур в начале и конце поверхности стены.
Пример. Внутри цилиндра А, поверхностью 2,5 кв. метров (черт. 31), циркулирует горячая вода, имеющая температуру вверху цилиндра 80° С., а внизу 60° С; наружная поверхность цилиндра служит для согревания воздуха, который подводится к низу цилиндра при температуре - 10° С. и, проходя около поверхности его, согревается до + 20° С.; коэффициент К передачи тепла от воды к воздуху через стенки цилиндра=8,0 ед. т.; требуется определить количество тепла, передающееся в течение 1 часа от воды к воздуху.
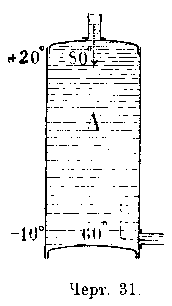
Для применения в этом случае формулы можно принять, что средняя температура воды в цилиндре равна
80+60/2=70 С а воздуха 20+(-10)/2=50С и тогда все количество тепла, передающееся от воды к воздуху в 1 час, будет:
W=FK(T-t)=2,5 X 8 X(70 - 5)=1300 ед. т.,
Но при большом изменении температуры среды, как это бывает напр. при циркуляции продуктов горения по дымооборотам печей, подобный прием дает уже весьма далекие от истинных результаты, почему для этих случаев необходимо применять другие более сложные, формулы. Не останавливаясь на выводе этих формул, укажу здесь лишь окончательный вид их для различных, встречающихся на практике, случаев. В общем случае вопрос может быть формулирован так: дана стена, с одной стороны которой движется постоянное количество горячих газов, передающих свою теплоту стене, вследствие чего температура их постепенно понижается; с другой стороны стены движется постоянное количество воздуха, согревающегося от стены, причем температура его постепенно повышается; требуется определить количество тепла, передающееся в 1 час от газов к воздуху через всю поверхность стены F, при условии установившейся передачи тепла, то-есть при условии, что через каждую точку поверхности стены во все время передачи тепла передается постоянное количество его.
Здесь могут встретитьcя следующие случаи:
1) Газы и воздух движутся по одному и тому же направлению (черт. 32), температура газов в начале T1 в конце Т2, температура воздуха в начале t1 -в конце t2, при чем:
T1>T2 и t2>t1
Количество тепла, передающееся в 1 час через F кв. м., будет:
W=FK(T1-T2+t2-t1) / lqnt((T1-t1) / (T2-t2))
2) Газы и воздух движутся по противоположным направлениям (черт. 33), при чем: Т1 >Т2 и t2 >t1; формула будет иметь тот же вид, с тою лишь разницею, что в ней вместо t1 будет t2 и наоборот; поэтому W=FK(T1-T2+t1-t2) / ((T1-t2)/(T2-t1))
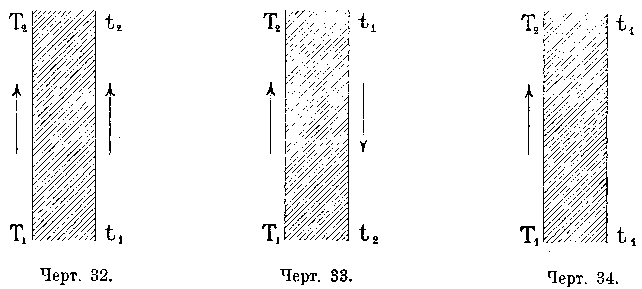
рисунок 32,33,34
3) Температура газов изменяется, воздух же находится в покое и температура его на всем протяжении поверхности постоянна, то-есть (черт. 34): T1>T2 и t1=t2; вставляя в вышеуказанную формулу вместо t2, получим:
W=FK(T1-T2)/((T1-t1)/(T2-t2))
4) Температура газов на всем протяжении поверхности не изменяется, температура же воздуха изменяется; в этом случае (черт. 35)T1=T2 и t2>t1 и почему:
W=FK(t2-t1)/((T1-t1)/(T1-t2))
5) Температуры газов и воздуха не изменяются на всем протяжении поверхности, то-есть:T1 = Т2 и
t1=t2; если и для этого случая подставит в формулу (15) Т1 вместо Т2 и t1 вместо t2, то получится неопределенная величина:
W=0/0
Истинное значение величины W в этом случае было уже найдено нами ранее и равно согласно формуле (14):
W=FK(T1-t1)
| (Нет голосов) |
Печник (Москва)





















